Modeling the Time-Periodic Groundwater Flow
Published on by Water Network Research, Official research team of The Water Network in Academic
In many cases groundwater systems are responding in whole or in part to time-periodic forcings – either natural or artificial. There is a pressing need for sound, physics-based understanding of time-periodic groundwater flow.
A time-periodic forcing is a boundary condition or internal source/sink whose time variation can be represented as a sum of periodic functions (sines and cosines).
An example is a coastal aquifer subject to tidal water-level variations at its seaward boundary.
Scientists and engineers routinely work with periodically forced groundwater systems for applications ranging from resource management to environmental remediation. This work usually consists of some combination of observation, analysis, and model building.
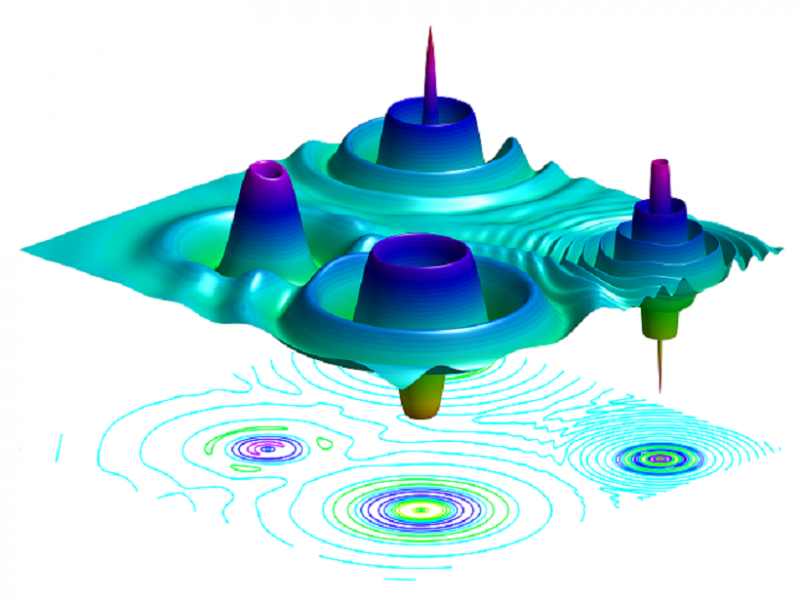
Image: 2-D model of water-level response in an aquifer due to periodic excitation of four groundwater wells at different amplitudes and frequencies.
Image source: EOS
Geoscientists have been studying periodically forced groundwater systems for decades, so the relevant literature is relatively abundant. Unfortunately, current groundwater hydrology and groundwater hydraulics textbooks simply don’t have sufficient space to discuss the theory of time-periodic groundwater flow in significant detail.
So there is, in effect, a large gap between the ideas presented in the research literature and current textbooks. Clearly then, there is a need for tutorial material that bridges this gap by presenting a comprehensive description of the basic theory. We wrote our book, Hydrodynamics of Time-Periodic Groundwater Flow, to satisfy this need.
Rather than focusing on the latest research findings, or reviewing the history of the subject (e.g., through a comprehensive literature review), we lay out the basic theory of time-periodic groundwater flow as it applies under a rather narrow set of simple conditions – homogeneous fluids moving through fully saturated, elastically deformable, porous media in which Darcy’s law is satisfied.
We leave the discussion of more advanced topics to subsequent efforts by other authors. Such topics include, for example, partially saturated media, inhomogeneous (variable-density) fluids, fractured media and non-Darcian flows.
Geologic media are frequently spatially variable with respect to material hydrologic properties (hydraulic conductivity and specific storage), and may be anisotropic with respect to hydraulic conductivity (e.g., due to distinct layering), so we incorporate spatially variability and anisotropy in our analyses whenever practical. As a result, many of the important theoretical results presented in the book apply to spatially variable, anisotropic media.
Hydrodynamics of Time-Periodic Groundwater Flow: Diffusion Waves in Porous Media, 2016
By Joe S. Depner and Todd C. Rasmussenon
Source: EOS
Media
Taxonomy
- Modeling
- Groundwater
- Hydrological Modelling
- Groundwater Assessment
- Groundwater Modeling
- Groundwater Mapping
- Hydrological Modelling
- Analytics & Modeling
- 3D Modelling